“Công nghệ” dạy toán mới trên thế giới: Khám phá quy tắc đại số trước khi đếm 1, 2, 3, 4... (Phần 3)

1.040

Trong phần 2, chúng ta đã biết trẻ em Mỹ và nhiều nước thường bắt đầu học toán bằng cách đếm số để nắm được 4 phép tính căn bản, rồi từ số học chuyển qua đại số. Ngoài cách tiếp cận phổ biến này thì trên thế giới lại có một cách tiếp cận môn toán hoàn toàn khác: bắt đầu môn toán từ việc đo chiều dài, thể tích và học khám phá các quy tắc đại số trước khi đến với các con số. Đó là cách dạy toán của đất nước đã sản sinh ra nhiều phát minh khoa học kỹ thuật làm thay đổi lịch sử nhân loại trong 300 năm trở lại đây.

Phương pháp dạy toán mới cụ thể là như thế nào và kết quả thử nghiệm phương pháp mới này tại Mỹ ra sao? Mời bạn đọc đến với phần 3:

"Công nghệ" thiết kế môn toán phát triển tư duy trừu tượng từ đại số đến số học của người Nga

Loạt bài dài kỳ này tổng hợp từ một bài viết của tác giả Keith Devlin trên website Hiệp hội toán Mỹ (MAA) và các nghiên cứu, tác phẩm liên quan. Keith Devlin là một nhà toán học nổi tiếng người Mỹ, cựu giáo sư toán đại học Stanford.

Thực nghiệm phương pháp dạy toán mới tại Mỹ

Cách tiếp cận từ đại số đến số học là phương pháp trong giáo trình đương đại bắt đầu bằng phép đo thay vì đếm số mà tác giả Keith Devlin đã nhắc đến trong phần 2.

Giáo trình sẽ là trọng tâm chính trong phần còn lại của loạt bài được phát triển trong nửa sau thế kỷ 20 với hai người đứng đầu là hai nhà giáo dục và tâm lý Vasily Davydov (1930-1988), D.B.Elkonin (Daniil Elkonin, 1904–1984).

Giáo trình Davydov ngày nay thường được gọi theo tên Davydov có sự tham gia đóng góp của nhiều người khác mà nổi tiếng nhất là D.B.Elkonin. Nền tảng của chương trình Elkonin-Davydov là các học thuyết nhận thức của Lev Semenovich Vygotsky (1896-1934), một nhà tâm lý phát triển lớn.

Vaisly Davydov, D.B. Elkonin và Lev Vygotsky đều là những nhà khoa học nổi tiếng đến từ nước Nga, quốc gia có nền toán học hàng đầu thế giới. Toán học và tư duy khoa học là nền tảng để đất nước này đi tiên phong sáng tạo ra nhiều phát minh khoa học kỹ thuật cho thế giới trong gần 300 năm trở lại đây: công nghệ máy tính, du hành vũ trụ, hệ thống đèn đường, máy bay trực thăng, vô tuyến truyền hình...

Hai trong số ít ỏi các nghiên cứu thực nghiệm chương trình toán tiểu học Davydov tại Mỹ được Keith quan sát đều cho kết quả rất phấn khởi.

Nghiên cứu đầu tiên do Jean Schmittau-giáo sư ngành sư phạm toán tại trường sư phạm đại học quốc gia New York ở Binghamton-dẫn đầu, áp dụng giáo trình toán tiểu học Davydov trọn bộ ba năm tại một trường ở New York.

Theo báo cáo, các trẻ tham gia có thể liên tục giải quyết vấn đề trong các thử thách đáng chú ý. Khả năng duy trì sự tập trung mạnh mẽ, điều kiện cần thiết cho thành công của các em cũng được phát triển dần. Thời gian cần thiết để học sinh đáp ứng được các thử thách là khoảng một năm.

Đáng ngạc nhiên là "khi hoàn thành chương trình, chúng có thể giải các bài toán thông thường chỉ dành cho học sinh trung học phổ thông Mỹ".

Một số ý kiến cho là, trong kỷ nguyên máy tính điện tử giá rẻ, trẻ em không cần học cách tính toán, và thời gian dành cho tính toán thật sự sẽ cản trở việc học toán về mặt khái niệm. Trước những lời phàn nàn này, giáo sư Schmittau cho rằng: "không thể chấp nhận quan điểm sự hình thành khái niệm và khả năng giải quyết các vấn đề khó lại phải thỏa hiệp với việc học tính toán. Các trẻ học chương trình Davydov không chỉ đạt được năng lực vận dụng quy tắc và kiến thức toán ở mức độ cao mà chúng còn có thể phân tích và giải các bài toán mà thông thường được xếp loại khó đối với học sinh trung học phổ thông Mỹ. Chúng không dùng máy tính, và chúng giải quyết được mỗi sai sót tính toán về mặt hình thành khái niệm mà không cần bám lấy các quy tắc".

Ngoài ra, khi thành thạo năng lực tính toán thì các em cũng phát triển được tư duy toán và khả năng thiết lập các kết nối mới, nền tảng của học tập có ý nghĩa.

Học tập có ý nghĩa còn gọi là học hiểu sâu, là việc hiểu rõ khái niệm, liên tưởng được kiến thức mới với kiến thức cũ và áp dụng kiến thức mới vào thực tiễn, trái với học thuộc lòng là chỉ đơn thuần ghi nhớ.

Nghiên cứu thứ hai tại hai trường ở Hawai'i sử dụng giáo trình Measure Up, một phiên bản của giáo trình Davydov dành cho trẻ em Mỹ trong dự án nhóm phát triển và nghiên cứu giáo trình (Curriculum Research & Development Group-CRDG) trường sư phạm đại học Hawai'i. Hai tác giả nghiên cứu là Barbara J. Dougherty, tiến sĩ ngành sư phạm toán, giám đốc CRDG và tiến sĩ Hannah Slovin là một thành viên CRDC.

Kết quả nghiên cứu thứ hai cũng rất khả quan "Các phương pháp giải quyết (vấn đề) nhấn mạnh rằng trẻ nhỏ có khả năng sử dụng các ký hiệu đại số và các sơ đồ được khái quát hóa để giải các bài toán. Các sơ đồ và ký hiệu liên quan có thể biểu diễn cấu trúc của một tình huống toán và được ứng dụng trong nhiều bối cảnh".

Ảnh chụp học sinh học chương trình toán Measure Up. (Ảnh: CRDG).

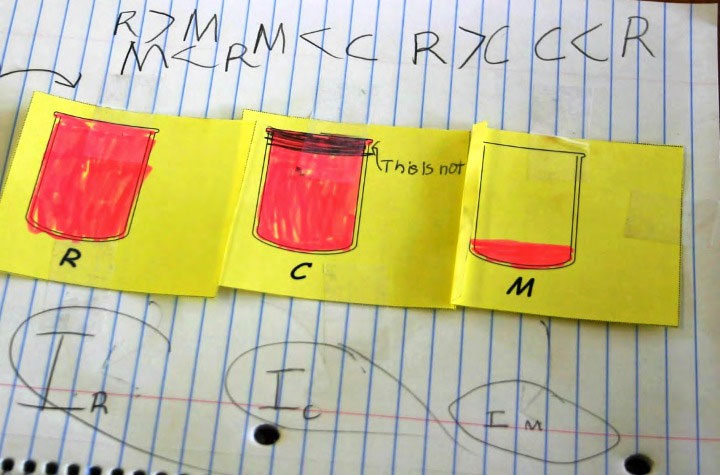
Ghi chú bằng ký hiệu đại số của học sinh học toán Measure Up. (Ảnh: CRDG).

Thiết kế môn toán phát triển tư duy đại số "trừu tượng" từ lớp 1

Giáo trình Davydov áp dụng cách tiếp cận thứ hai: các con số cụ thể là sự trừu tượng hóa các kết quả đo lường. Tuy vậy, nếu chỉ đo đạc chiều dài một vật nào đó hay đếm số lượng một nhóm đồ vật nào đó thì chúng ta chỉ có được khái niệm tự phát (spontaneous concepts) về số. Phương pháp Davydov còn gọi là phương pháp khái niệm khoa học (scientific concepts). Theo phương pháp này, để có khái niệm khoa học về số thì học sinh cần trải qua một giai đoạn tiền-số trước khi học các con số cụ thể.

Dưới đây là miêu tả chương trình Davydov theo tác phẩm Logical and psychological problems of elementary mathematics as an academic subject (Các vấn đề logic và tâm lý trong toán tiểu học, một môn học học thuật) bản in 1975a.

Phần đầu tiên trong lớp học là các bài tập không liên quan đến số (non-numerical) về kích thước như chiều dài, thể tích, khối lượng được thiết kế theo hướng tăng dần độ phức tạp.

Bước đầu tiên là bước "tiền toán học" để chuẩn bị cho học sinh làm các bài tập này.

Ở lớp 1, giáo viên sẽ yêu cầu học sinh mô tả và xác định các đặc điểm vật lý (chiều dài, thể tích, khối lượng) của một số đối tượng có thể so sánh được.

Trong giai đoạn này, khi mô tả kết quả, học sinh sẽ viết các mệnh đề như A > B, B = C, A > C. A và B là những đại lượng chưa xác định đang được so sánh.

Ở bước này, những đại lượng chưa xác định không phải là con số cụ thể. Việc sử dụng ký hiệu đại số (ở đây là ký tự chữ cái) trước khi dùng các ký hiệu số sẽ giúp học sinh tập trung ngay vào các trừu tượng hóa từ lúc đầu. Tình huống vật lý được tạo ra để giới thiệu các yếu tố đại số "trừu tượng" một cách có ý nghĩa, trẻ nhỏ không thấy chúng trừu tượng mà rất thực tế.

Ảnh minh họa tình huống so sánh thể tích.

Mục đích của tình huống trên là giúp trẻ khám phá các quan hệ bằng nhau, quan hệ so sánh.

Tiếp theo là bài tập về quan hệ bộ phận-toàn thể. Học sinh học cách biến các đại lượng không bằng nhau trở thành bằng nhau hay biến các đại lượng bằng nhau trở thành không bằng nhau.

Từ tình huống thể tích A > B, trẻ có thể đạt được sự cân bằng bằng cách cộng thêm vào thể tích B hay trừ đi từ thể tích A. Rồi các em quan sát rằng, dù lựa chọn cộng hay trừ thì lượng cộng thêm hay trừ đi cũng giống nhau, và lượng đó được gọi là sự chênh lệch-một trong những khái niệm toán học đầu tiên mà học sinh của chương trình được học.

A > B
A = B + X
X = A – B
A = B + (A – B)

Chỉ sau khi học sinh đã thành thạo kiến thức tiền-con số về kích thước và các quan hệ bộ phận-toàn thể, các em mới tiếp tục những nhiệm vụ yêu cầu lượng hóa.

Ví dụ, sau khi làm việc với khối lượng và thấy rằng, khối lượng Y là toàn thể và các khối lượng A và Q là những bộ phận tạo nên tổng thể, các em được khuyến khích thể hiện điều đó bằng một sơ đồ đơn giản hình chữ V lộn ngược như thế này:

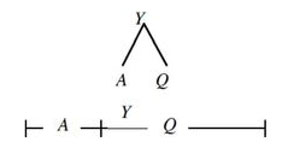
Rồi tiếp tục viết lại các biểu thức theo những cách hình thức hơn:

Y = A + Q, Q + A = Y, Y - Q = A, Y - A = Q

Các biểu thức trên mở đầu cho giai đoạn đặt giá trị số xác định cho các "biến" để giải các phương trình xuất phát từ các bài toán thực tiễn.

Số (ở đây là số thực) được giới thiệu trong nửa sau của lớp một như các phép đo trừu tượng của chiều dài, thể tích, khối lượng và những thứ tương tự.

Kết quả là, học sinh không những không cần học thuộc các quy tắc giải phương trình đại số mà còn gia tăng khả năng lập luận trực tiếp về các mối quan hệ bộ phận-toàn thể.

Đến phép nhân và chia, giáo trình Davydov yêu cầu học sinh kết nối các hành động nhân, chia mới với kiến thức trước đó về phép đo và giá trị của hàng chữ số (place value), cộng và trừ, và áp dụng phép nhân và chia vào các bài toán liên quan đến hệ đo lường, các hệ cơ số khác (các hệ cơ số khác ngoài hệ thập phân được dạy ở lớp 1), diện tích và chu vi, cách giải các phương trình phức tạp hơn.

Một bài tập trong chương trình toán tiểu học Davydov tại Mỹ. (Ảnh: CRDG).

Nói cách khác, các em học được các phép toán mới từ cơ sở thực tiễn lẫn sự kết nối với kiến thức toán đã học trước đó. Học sinh phải khám phá hai phép toán mới và các xuyên liên hệ mang tính hệ thống giữa chúng và các khái niệm đã học trước đó. Chúng liên tục được giới thiệu các bài toán mà chúng phải xây dựng kết nối với các kiến thức cũ.

Mỗi bài toán mới có khác biệt với những bài toán trước và sau đó theo một số cách có ý nghĩa thực tế. Điều này trái ngược với chương trình Mỹ, các vấn đề được trình bày theo tập hợp với mỗi tập hợp tập trung vào một tiến trình duy nhất.

Kết quả là, học sinh phải liên tục suy nghĩ về những gì chúng đang làm để làm cho điều đó trở thành hiện thực với chúng. Nhiều bài toán được thiết kế như vậy giúp trẻ xây dựng kết nối giữa các hành động mới (nhân và chia) với kiến thức trước đó về cộng trừ, các hệ thống số định lượng theo vị trí (positional system), phương trình. Tất cả những bài toán này sẽ giúp trẻ tích hợp được kiến thức của mình vào một hệ thống khái niệm duy nhất.

Theo Keith, giáo trình Davydov có cơ sở từ thực tiễn, nhưng điểm bắt đầu là thế giới đo lường có tính liên tục hơn là thế giới đếm rời rạc.

Cả phép đo lẫn phép đếm đều đem lại những điểm bắt đầu cụ thể tốt đẹp cho hành trình toán học. Con người được sinh ra với năng lực đưa ra nhận xét và lập luận về chiều dài, diện tích, thể tích… cũng như năng lực so sánh kích cỡ các nhóm đồ vật. Mỗi năng lực đều trực tiếp dẫn tới một khái niệm số nhưng là hai khái niệm khác nhau tương ứng với số thực và số đếm.

(Còn tiếp)...

Cập nhật: 12/09/2019 Theo vnreview