Bài toán siêu khó tồn tại hàng thập kỷ đã được giải, đáp án nặng tới 200TB

Dung lượng khổng lồ chỉ để chứa lời giải cho một bài toán. Thực sự bài toán đó khó vậy sao?

Hẳn là nhiều người trong chúng ta mất nhiều năm trời học qua cấp 1, cấp 2 và cấp 3 để thoát khỏi môn Toán (để rồi lên Đại học lại dính phải Toán Cao Cấp). Các bạn nghĩ bài tập toán giao về nhà sau mỗi tiết học là khoai ư? Vậy thì các bạn hãy nhìn vào bài toán này đây, để giải nó cần tới 3 nhà toán học và 200 terabyte dung lượng chỉ để chứa lời giải, đấy là đã có một siêu máy tính giúp sức rồi đấy nhé!

Bạn cứ tính, 1 terabyte chứa được 337.920 bản Chiến tranh và Hòa Bình, bộ tiểu thuyết của Lev Tolstoi, bộ tiểu thuyết dài nhất trong lịch sử loài người, vậy thì 200 terabyte sẽ chứa lượng chữ nhiều khủng khiếp đến nhường nào.

Bài toán này khó đến mức nào mà bài giải lại vĩ đại tới vậy? Đó là một vấn đề toán học xoay quanh định lý Pythagoras (hay chúng ta vẫn biết nó dưới tên định lý Py-ta-go), được đưa ra lần đầu tiên bởi giáo sư toán học Ronald Graham hồi những năm 1980. Có tên là Biến số đúng sai của bộ ba số nguyên dương Pythagoras (Boolean Pythagorean Triples), vấn đề toán học này "khoai" đến mức Graham đã treo giải 100 USD cho bất kì ai giải được (năm 1980 nhé!).

Vấn đề toán học này xoay quanh công thức của định lý Pythagoras: a^2 b^2 = c^2. Trong đó a và b là hai cạnh góc vuông của một tam giác vuông, còn c là cạnh huyền.

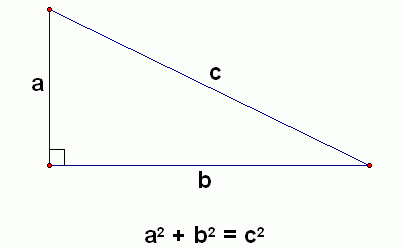
Công thức của định lý Pythagoras.

Giải thích về tên của vấn đề toán học này:

Bolean là biến có giá trị đúng hoặc sai.

Còn về Pythagoras Triples, có những bộ số nguyên dương được gọi là bộ ba Pythagoras sẽ luôn đúng khi áp dụng vào công thức của Pythagoras như: 3^2 4^2 = 5^2; 8^2 15^2 = 17^2. Chúng được gọi là Bộ ba số nguyên dương Pythagoras.

Và bạn hãy tưởng tượng rằng mọi số nguyên dương trong bảng chữ số sẽ được tô màu hoặc đỏ hoặc xanh. Graham đã đưa ra bài toán rằng: liệu có khả thi không khi thực hiện việc tô màu mọi số nguyên hoặc xanh hoặc đỏ, để cho không có Bộ ba pythagoras nào có cùng màu. Và 100 USD sẽ được thưởng cho bất cứ người nào giải được bài toán ấy (Chà, với 100 USD thì ta có thể chi trả cho tận 1 cái ổ có dung lượng 1 terabyte).

Ronald Graham, người thầy đã giao cho chúng ta bài toán mà mãi hàng thập kỉ sau mới có thể giải được.

Vấn đề toán học này khó ở chỗ: một số nguyên dương có thể nằm trong nhiều Bộ Ba Pythagoras khác nhau. Ví dụ như số 5, ta có dãy 3-4-5 là Bộ Ba Pythagoras, nhưng dãy 5-12-13 cũng vậy. Áp dụng điều kiện của Graham, nếu số 5 của dãy đầu tiên tô màu xanh, thì trong dãy thứ hai nó cũng phải là màu xanh, vì thế số 12 và 13 phải mang màu đỏ.

Càng tiến xa hơn với điều kiện mà Graham đề ra, các con số càng lớn và vấn đề bắt đầu nảy sinh. Nếu như số 12 phải mang màu đỏ trong dãy 5-12-13, những dãy số sau này chứa số 12 sẽ bắt buộc mang một màu nhất định.

Các nhà toán học Marijn Heule từ Đại học Texas, Victor Marek từ Đại học Kentucky, và Oliver Kullmann từ Đại học Swansea tại Anh đã cùng nhau giải quyết vấn đề này. Họ đã cài đặt một số phép thử và kĩ thuật tính toán vào trong siêu máy tính Stampede tại Đại học Texas, để cho nó có thể thu hẹp phạm vi "tô màu" xuống còn 102,300 tỷ tỷ khả năng (trăm nghìn tỷ tỷ, từng đó là có tổng cộng 25 số "0" đó các bạn).

Dàn siêu máy tính Stampede được sử dụng để giải bài toán khó này.

Bộ siêu máy tính gồm 800 vi xử lý mạnh mẽ đã phải mất tới 2 ngày để "nhằn" hết đống phép thử kia, và nó chỉ có thể khả thi cho tới số 7.824. Bắt đầu từ 7.825 trở đi là không thể thỏa mãn điều kiện đặt ra của Graham.

Vậy là 3 nhà toán học (kèm một cái siêu máy tính) đã giải quyết được vấn đề toán học đã tồn tại cả thập kỉ này, và cụ Ronald Graham cũng đã giữ lời hứa của mình, thưởng "hậu hĩnh" món tiền 100 USD cho 3 anh.

"Bộ ba nguyên tử" của 3 nhà toán học này đã tạo ra một bản nén 68 gigabyte cho bất kì bạn trẻ nào có một bộ vi xử lý tốt cùng với 30.000 giờ rảnh rỗi để tải về, tái dựng và xác minh vấn đề. Nhưng nếu bạn có 30.000 giờ rảnh thật thì cũng còn một vấn đề khác nữa, con người không thể đọc được những dòng thuật toán đó.

Thực tế, bộ ba đã phải "nhờ" một chương trình máy tính khác để xác minh lại kết quả của họ, và cuối cùng thì 7.824 là con số chính xác. Ronald Graham cũng hài lòng với việc xác minh được con số này.

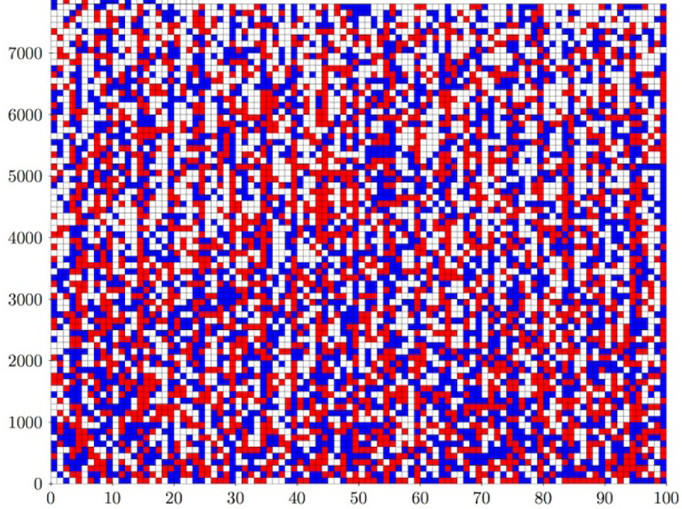
Các số từ 1 cho tới 7,824 có thể được tô màu bởi chúng thỏa mãn điều kiện của Graham đưa ra. Nhưng từ 7,825 trở đi, không có số nào thỏa mãn cả.

Nhưng nhiều người cho rằng, con người không đọc nổi kết quả nên nó không đủ thuyết phục. Dù không chứng minh được là nó sai, nhưng việc đó cũng không giải quyết vấn đề đến tận cùng. Tại sao bắt đầu từ số 7.825 trở đi thì việc "tô màu" là bất khả thi? Chúng ta không giải thích được, mà chỉ được dàn siêu máy tính kia cho biết vậy thôi.

Làm sau mà con người có thể hiểu được ý nghĩa của các con số với chúng ta cũng như với cả Vũ trụ nếu như mọi vấn đề toán học được giải quyết bằng máy như vậy. Sự thực là vấn đề này quá khó giải quyết, có lẽ cũng lại phải nhờ một bộ siêu máy tính nào đó vào cuộc thôi.