Dãy số Fibonacci và tỷ lệ vàng: bí ẩn của Vũ trụ hay chỉ đơn giản là sự trùng hợp?
Dãy số này xuất hiện ở muôn nơi: trong tự nhiên và cũng như từ các sản phẩm nhân tạo, từ vũ trụ cho tới bài nhạc cổ điển.
Số Phi ((Φ,φ) ), số Fibonacci, tỷ lệ vàng là những khái niệm rất nổi tiếng và quen thuộc, đã được các nhà toán học nghiên cứu xuyên suốt lịch sử, từ thời điểm đầu tiên khi nó xuất hiện. Đó là một dãy vô hạn các số tự nhiên bắt đầu bằng hai phần tử 0 và 1 hoặc 1 và 1, các phần tử sau đó được thiết lập theo quy tắc mỗi phần tử luôn bằng tổng hai phần tử trước nó.
Thậm chí, trái với định kiến toán học là khô khan, khái niệm số Fibonacci xuất hiện trong vô vàn lĩnh vực khác như nghệ thuật, sinh học, kiến trúc, âm nhạc, thực vật học và thậm chí, cả tài chính. Rất có thể, bạn đã tiếp xúc với số Fibonacci đâu đó trong sự nghiệp học tập và nghiên cứu rồi. Liệu bản chất của nó có đi kèm với ý nghĩa rằng: Ta có thể tìm ra được một bản dịch thuật được viết bằng số của mọi thứ ta nhìn thấy, ta nghe được – vạn vật xung quanh ta không?
Có lẽ câu trả lời gần với câu hỏi này nhất là câu nói của triết gia vĩ đại Plato, “Chúa trời vận dụng hình học không ngừng nghỉ - God geometrizes continiually”. Rất xin lỗi nếu như khả năng hạn hẹp của tôi không thể dịch ra được một câu hay hơn.

Plato.
Giờ hãy nhìn sâu hơn vào hiện tượng toán học thu hút hàng ngàn trí thức gia và học giả từ mọi ngành, mọi kỷ nguyên kể từ lần đầu tiên nó được phát hiện ra: vậy đó là tỷ lệ vàng hay là sự cân xứng thần thánh?. Trước khi bắt đầu chuyến hành trình này, ta hãy lật lại câu chuyện về nhà toán học người Ý Leornardo Bigollo (Leonardo Pisano hay “người tới từ Pisa”), ông Fibonacci.
Đường xoắn ốc Fibonacci
Số Phi được gọi là Phi là bởi nó được đặt theo tên nhà điêu khắc nổi tiếng người Hy Lạp Phidias (sống tại thế kỷ thứ 5 Trước Công nguyên). Ông là người kiến tạo nên những công trình kiến trúc nổi tiếng, trong đó có đền Parthenon tại Athens. Teho như tác giả Mario Livio viết trong cuốn sách Tỷ lệ Vàng: Câu chuyện về Phi, Con số Kì diệu nhất Thế giới, rất nhiều nhà sử học tin rằng Phidias đã áp dụng thành công tỷ lệ vàng vào trong những tác phẩm của mình.

Phidias.
Đó là lý do vì sao nhà toán học Mark Barr quyết định vinh danh Phidias bằng cách đặt tên biểu tượng Φ là Phi. Vì thế, Phi chẳng phải là khám phá được tìm ra bởi Fibonacci (nó cũng đã từng được nghiên cứu và định nghĩa bởi Euclid rồi) và cái tên Phi cũng chẳng mang chút “hương vị nước Ý” nào cả (vị spaghetti chăng?).
Dù vậy, ta vẫn cần phải tìm hiểu thêm khám phá của Fibonacci để có thể hiểu hơn về tiềm năng cân đối tuyệt vời của số Phi và những con số phát sinh từ nó. Sự thành công của Fibonacci và con số tỷ lệ vàng là hai mặt của cùng một đồng xu.
Dãy số Fibonacci được khám phá ra bởi “nhà toán học tới từ Pisa"– dãy 0;1;1;2;3;5;8;13 ... – thuộc lĩnh vực số học, ngành nghiên cứu các con số và những biến đổi cơ bản có thể thực hiện được với những con số ấy. Tỷ lệ vàng, được biểu diễn bằng cái tên Phi (có biểu tượng là Φ, φ) đến từ một thành công trong ngành số học, biểu diễn mối quan hệ của hai yếu tố có trên một đoạn thẳng. Đúng vật, Phi có một cấu trúc hình học được biểu thị như hình dưới đây:

Chúng ta sử dụng đại số học để tìm ra giá trị số của Phi (Φ), chúng ta sử dụng công thức đơn giản là Φ=a/b. Ta áp dụng công thức này lên biểu diễn hình học của hình ảnh trên, khi lấy tổng chiều dài đoạn thẳng (a+b) chia cho đoạn dài hơn (a), ta cũng ra được cùng kết qua khi lấy đoạn dài hơn (a) chia cho đoạn ngắn hơn (b). Tổng kết lại, ta có Phi (Φ) = (a+b)/a = a/b.
Kết quả của đẳng thức này là 1,6180339887..., cùng giá trị với tỷ lệ vàng được định nghĩa bởi nhà toán học Euclid, dưới lời mô tả của Mario Livio là “một con số vô tận và không lặp lại”.
Đáng tò mò thay, con số này lại rất giống với kết quả khi chia bất kì con số liên tiếp nào trong dãy Fibonacci cho nhau (ví dụ 5/3=1,666; 13/8=1,625). Kết hợp hai yếu tố này lại, ta đã thành công trong việc sử dụng hình học để biểu thị một phạm trù số học.
Đây là điểm làm cho bài viết này thú vị, chẳng cần tới một nhà toán học để có thể hiểu và thấy được cái đẹp của đại số. Hơn nữa, ta lại hiểu thêm được tính chất số học cơ bản nằm trong khám phá của nhà toán học đại tài tới từ Pisa: đường xoắn ốc Fibonnaci nổi tiếng.
Là điểm cân bằng của tự nhiên, là khoa học của những con số hay chỉ là một sự trùng hợp?
Các đặc tính của số Phi làm chúng ta vô cùng ngạc nhiên, và việc phát hiện ra nó dưới dạng tỷ lệ vàng đã cho ta một lối đi để phân tích những hình thái, những vật thể, những biểu thị hình học và thậm chí là những chuyển động trong tự nhiên vẫn diễn ra trong thế giới này. Nó lại đưa ra tới một câu nói đã được nêu ra đâu đó trong bài viết này: tỷ lệ vàng hay là sự cân xứng thần thánh.
Trong những hình ảnh trên, ta thấy đường xoắn ốc Fibonacci, hình chữ nhật với tỷ lệ vàng nhưng ngoài ra, nó cũng có thể dùng để xác định tam giác tỷ lệ vàng hay hình ngũ giác. Nhưng chúng đều có một điểm chung: chúng đều có “yếu tố vàng” ở trong mình.
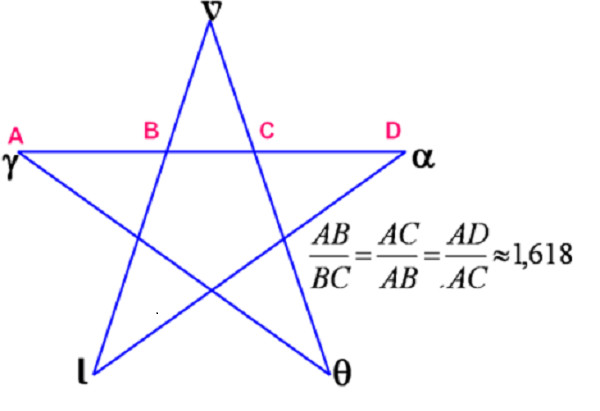
Hình ngũ giác với tỷ lệ vàng.
Mấy con số tỷ lệ vàng này là ta tự tạo ra, liệu môi trường xung quanh ta có “vàng” thế hay “thần thánh” thế không? Những công trình kiến trúc có tỉ lệ vàng là do con người tự làm nên, Mẹ Thiên nhiên có áp dụng công thức ấy trong việc kiến tạo không?
Câu trả lời là có. Ta có thể thấy tỷ lệ vàng trong Kim tự tháp Giza tại Ai Cập, trong logo của Google, hay trong những cánh hoa hồng và thậm chí, trong hình dáng của các ngân hà. Trong tác phẩm La Gioconda – tên gọi khác của bức Mona Lisa vẽ nên bởi Leonardo da Vinci, trong cấu trúc hiển vi của một số tinh thể, và thậm chí (lần 2), có cả trong bản nhạc Dialogue du vent et la mer của nhà soạn nhạc Claude Debussy – dãy số Fibonacci xuất hiện 50 bar nhạc, có thể được chia ra thành những đoạn dài 21, 8, 8, 5, và 13 bar.

Tỷ lệ vàng của bức La Gioconda.

Tỷ lệ vàng của ngân hà.
Sự xuất hiện của dãy số, của tỉtỷlệ vàng kì diệu này ở muôn nơi. Vậy ta gọi nó là con số thú vị nhất thế giới đã đủ xứng đáng chưa? Liệu dựa vào con số này, ta có thể thay đổi được thực tại để làm những điều không tưởng, tạo ra một thế giới không-còn-toán-học không? Nhưng không nghi ngờ gì, những sự thật này cho ta thấy rằng toán học khiến ta cảm thấy những thứ dường như không liên quan gì tới nhau lại có một điểm chung kì lạ: một dãy số níu giữ chúng lại.
Khám phá
-

Tàu Trung Quốc xác định “thế giới ngầm” khó tin trong Mặt trăng
-

NASA phát hiện mỏ đá quý trên sao Hỏa, sinh vật ngoài hành tinh đang "canh giữ"?
-

Phát hiện chấn động về tình trạng "kết hôn cận huyết" tại Hy Lạp thời cổ đại
-

Chỉ với một câu lệnh, AI mới sẽ tạo ra video chân thực như thế này
-
Chuyến trở về mạo hiểm đánh dấu mốc lịch sử của 4 phi hành gia tư nhân
-

Tàu thăm dò Chang'e 5 phát hiện chất bí ẩn trên Mặt trăng
Khám phá khoa học
-

Sự thật của các lầm tưởng hoang đường về thời Trung Cổ
-

Món đồ nào của Einstein được đấu giá triệu đô?
-

Những người thích chọc tức người khác
-

Phụ nữ nóng tính dễ bị đánh giá thấp
-

Chúng ta có thể ngừng suy nghĩ không?
-

3 bí kíp tính bằng tay "như hack" đáng để truyền cho muôn đời sau