Emmy Noether: Người phụ nữ đã phát triển một trong những định lý đẹp nhất trong vật lý
Các định luật bảo toàn rất hữu ích cho vật lý. Về cơ bản, khi một đặc tính có thể đo lường cụ thể của một hệ vật chất cô lập không thay đổi theo thời gian (và nó được bảo toàn), thì điều đó được mô tả bằng định luật bảo toàn.
Các định luật bảo toàn hữu ích trong một số lĩnh vực vật lý khác nhau, nhưng đôi khi, chúng có thể trở nên rất phức tạp. Đó là nơi mà một định lý những năm 1910 do một nhà toán học nữ người Đức phát triển trở nên hữu ích. Định lý Emmy Noether kết nối các định luật đối xứng và bảo toàn, và nó có thể được mô tả là một trong những định lý đẹp nhất trong vật lý.

Chân dung Emmy Noether khoảng năm 1900.
Amalie Emmy Noether là một nhà toán học người Đức có công việc đặc biệt tập trung vào đại số. Công việc của bà cũng có ảnh hưởng cực kỳ lớn trong một nhánh gọi là vật lý toán học - ngành liên quan đến sự phát triển của các phương pháp toán học trong vật lý.
Sự phát triển của nhiều định luật vật lý dựa trên một thứ rất trừu tượng, đó là khái niệm đối xứng. Đối xứng có thể có nghĩa là những thứ khác nhau trong các lĩnh vực khác nhau; trong hình học, các hình dạng hình học có thể đối xứng, trong hóa học, các phân tử có thể đối xứng, nhưng đối xứng cũng có nghĩa là một cái gì đó khác trong vật lý.
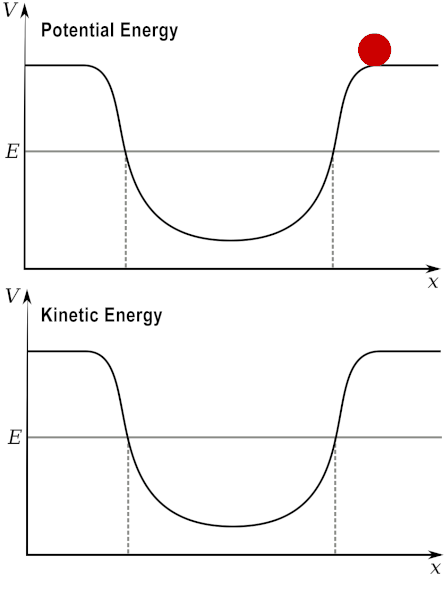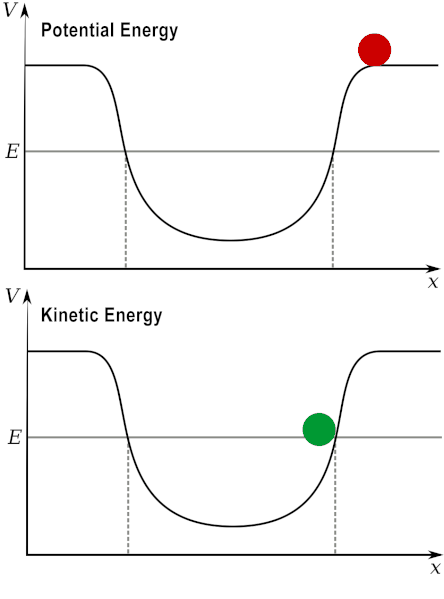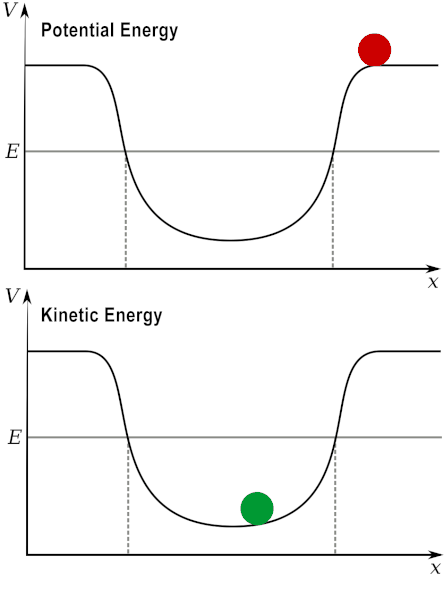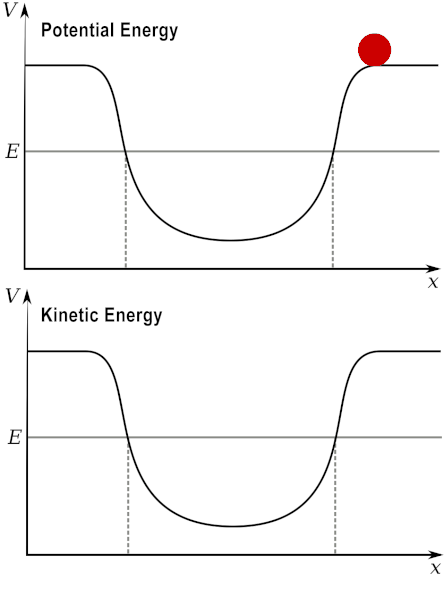
Nếu ném quả cầu lên cao với vận tốc ban đầu thì động năng sau đó sẽ chuyển thành thế năng. Hãy nghĩ về nó theo cách này: động năng phụ thuộc vào chuyển động, thế năng phụ thuộc vào vị trí; khi bạn ném quả bóng lên, nó bắt đầu bằng rất nhiều năng lượng chuyển động - nó sẽ đi lên. Sau đó, khi nó đạt đến độ cao tối đa, nó không có năng lượng chuyển động, bởi vì nó dừng lại (và sau đó đi xuống) - tại thời điểm đó, nó chỉ có thế năng.
Nói cách khác, thế năng biến đổi thành động năng, và động năng chuyển thành thế năng, rồi lại quay trở lại.
Nếu bạn thiết lập một thí nghiệm động năng-thế năng, thí nghiệm sẽ hoạt động như cũ nếu bạn thử lại trong cùng một điều kiện. Và trong những lần thực hiện tiếp theo ở thời gian sau đó, bạn vẫn sẽ nhận được điều tương tự - điều này có nghĩa là mức bảo toàn năng lượng là như nhau bất kể thời gian. Nói cách khác, sự biến đổi thời gian hoàn toàn không thay đổi hệ thống. Trường hợp không có gì thay đổi trong quy luật vật lý/ tính năng của một hệ thống ngay cả với hành động của một phép biến đổi được gọi là đối xứng.
Năm 1918, Emmy Noether xuất bản một bài báo kết nối các đối xứng và các định luật bảo toàn. Sau đó, sự nghiệp của nhà toán học người Đức này đã có những dấu hiệu phát triển rực rỡ. Mối quan tâm của bà đối với toán học đến từ cha của mình, một giáo sư toán học tại Đại học Erlangen. Sau đó, Noether tiếp tục trở thành một sinh viên và cũng là một giáo sư - nhưng làm việc không có lương. Emmy Noether ít được biết đến dù có những đóng góp to lớn cho khoa học thời điểm bấy giờ, Định lý Noether đã thống nhất các ý tưởng được René Descartes, Gottfried Leibniz, Isaac Newton và Joseph-Louis Lagrange phát triển chậm rãi hàng thế kỷ.
Chưa dừng lại ở đó, Noether đã xuất bản một bài báo toán học quan trọng thảo luận về các nhóm biến đổi, nhưng không thảo luận về mối quan hệ trực tiếp với vật lý. Công trình của bà được chia thành hai định lý, định lý đầu tiên đưa ra mối quan hệ toàn cục giữa các phép đối xứng liên tục và các định luật bảo toàn, trong khi đó, định lý thứ hai áp dụng cho các hệ có đối xứng cục bộ .
Thí nghiệm về quả cầu liên quan đến định luật bảo toàn là một ví dụ đơn giản nhất. Năng lượng được bảo toàn vì có sự đối xứng trong phép tịnh tiến theo thời gian. Bây giờ hãy xem xét một ý tưởng phức tạp hơn về sự bảo toàn momen động lượng (động lượng của một vật thể quay). Những vận động viên trượt băng là bậc thầy của việc bảo tồn này: họ biết rằng nếu họ quay với cánh tay úp vào, điều này sẽ làm cho họ quay nhanh hơn - và nếu họ mở rộng cánh tay, tốc độ quay của họ sẽ giảm.
Hãy nghĩ về nó theo cách này: momen động lượng là khối lượng nhân với vận tốc nhân với bán kính (L = m * v * r). Khối lượng của một vận động viên trượt băng không đổi, vì vậy nếu bán kính tăng lên, tốc độ phải giảm để bù đắp cho điều đó, và ngược lại.

Vận động viên trượt băng.
Vậy đối xứng trong trường hợp này là gì? Nếu động lượng được bảo toàn, thì không gian phải là đẳng hướng. Điều đó có nghĩa là nếu không có momen phụ (lực góc) thì momen động lượng không thay đổi. Nói một cách đơn giản, đẳng hướng có nghĩa là mọi thứ đều giống nhau ngay cả khi bạn xoay chúng. Ví dụ, một hình cầu hoàn hảo, không có bất kỳ vết nào, là bất biến khi quay, cho dù bạn quay nó theo cách nào, nó trông vẫn có hình dạng giống nhau.
Dù tin hay không, điều này liên quan đến một trong những lý thuyết quan trọng nhất trong vật lý: thuyết tương đối rộng.
Vật chất bẻ cong không-thời gian
Thuyết tương đối rộng (GR) là lý thuyết mô tả lực hấp dẫn với độ chính xác cao. Trong quá trình phát triển của nó, Emmy Noether đã đóng góp vào việc giải thích lý thuyết.
Từ năm 1915 đến năm 1918, bà đã tham gia vào các cuộc tranh luận với David Hilbert, Felix Klein và chính Einstein về các phương trình bảo toàn trong GR. Einstein đã đưa ra một biểu thức khá giống với biểu thức bảo toàn năng lượng mà chúng ta quen thuộc hơn. Tuy nhiên, một thành phần của phương trình là bất biến dưới một phép biến đổi cụ thể được gọi là phép biến đổi affine. Phép biến đổi affine bảo toàn cấu trúc song song giống như một lá đối xứng. Điều này không được mong đợi từ một phương trình tổng quát được cho là kết hợp bức tranh lớn về bảo toàn năng lượng.

Năm 1918, Klein đã chỉ ra sự khác biệt giữa phương trình trường của Einstein và sự bảo toàn năng lượng thông thường. Einstein không đồng ý, ông tin rằng sự bảo toàn tương tự như cơ học cổ điển ít nhất là một phần trong các phương trình của ông.
Đối với Hilbert, một nhà toán học hàng đầu trong thời đại của ông, thực tế là GR không cho thấy một kiểu bảo toàn năng lượng tương tự đơn giản là vì… nó là như vậy. Noether, và sau này là Klein, đồng ý rằng không có định luật bảo toàn trong Thuyết tương đối rộng, và kết luận đó xuất phát từ định lý nổi tiếng của bà.
Từ định lý thứ hai của Noether, vật chất trong GR cho thấy một sự bảo toàn tương tự như sự bảo toàn năng lượng và động lượng, nhưng không có phương trình chuyển động. Trên thực tế, bất kỳ lý thuyết nào giống nhau đối với bất kỳ hệ tọa độ nào đều cho thấy một định luật bảo toàn kỳ lạ, một định luật không đưa ra lời giải bằng các diễn giải vật lý trực tiếp.
Siêu đối xứng
Định lý đối xứng của Noether sau đó cũng được ứng dụng trong một số lĩnh vực vật lý khác.
Mô hình chuẩn của vật lý hạt chia các hạt thành hai loại: fermion và boson. Tất cả các fermion đã biết (các hạt cấu tạo nên vật chất thông thường) đều có spin bán nguyên. Số spin mô tả có bao nhiêu mặt đối xứng mà một hạt có trong một lần quay hoàn toàn; spin bằng 1/2 có nghĩa là hạt phải được quay đủ hai vòng (qua 720°) trước khi nó có cấu hình giống như khi nó bắt đầu.
Trong khi đó, boson, không phải là hạt vật chất, có spin nguyên (0, 1, 2, v.v.). Spin là một đặc tính ở các hạt cho biết chúng sẽ chỉ ở đâu nếu được nhúng trong từ trường. Một lý thuyết được đề xuất được gọi là Siêu đối xứng (SUSY) cho rằng cứ mỗi fermion được phát hiện sẽ có một boson siêu đối xứng với đặc tính tương tự.
Nó làm cho mọi thứ trở nên chắc chắn hơn, nhưng nó cũng làm cho mọi thứ trở nên đơn giản hơn nhiều. Hạt nhẹ nhất của SUSY sẽ tạo nên một hạt vật chất tối tuyệt vời. Hơn nữa, các hạt khác có thể được dự đoán từ SUSY, mặc dù không phải trong số chúng đã được quan sát bằng thực nghiệm.
Theo định lý Noether, có thể tìm được sự bảo toàn nếu nó được kết nối với phép đối xứng. Số lượng bảo toàn của SUSY là phụ phí, một số loại ý tưởng chung về phí như chúng ta hiểu.
Sự công nhận
Những đóng góp của bà cho toán học là rất lớn, đặc biệt là liên quan đến cuộc đời ngắn ngủi của bà.
Noether phải vật lộn trong một xã hội phân biệt giới tính như hầu hết các nhân vật nữ khoa học khác vào thời của mình. Là một trong những nhà khoa học lỗi lạc nhất, tài năng chính là điều cơ bản nhất trong việc khiến các đồng nghiệp của Noether tôn trọng. Nhưng điều đó vẫn chưa đủ.
Thật không may, Noether vẫn cần sự hỗ trợ - hoặc có thể chúng ta nên gọi đó là sự chấp thuận - của những nhà toán học quan trọng được các trường đại học coi trọng. Hilbert đã tham gia vào việc đó, ông thuyết phục những người khác chấp nhận bà tại Göttingen, nói rằng “Tôi không thấy rằng giới tính là rào cản khiến chúng ta không công nhận tài năng của cô ấy”.
Định lý Noether được gọi là “một trong những định lý toán học quan trọng nhất từng được chứng minh trong việc hướng dẫn sự phát triển của vật lý hiện đại”. Những đóng góp của bà cho toán học là rất lớn, đặc biệt là liên quan đến cuộc đời ngắn ngủi của bà. Bà đã khám phá ra một trong những ý tưởng thanh lịch nhất, và có thể là sâu sắc nhất trong vật lý hiện đại, thường phải đối mặt với nghịch cảnh lớn từ các lĩnh vực do nam giới thống trị. Đó là một trong những điều hoàn toàn đáng biết nếu bạn quan tâm đến khoa học.
Sự kiện
-

Cơ thể "khóc thét" ra sao nếu bạn uống quá nhiều bia mỗi ngày?
-

Kính viễn vọng của NASA chụp được vật thể "lẽ ra không tồn tại"
-

Phát hiện “rung chuyển” ở hành tinh mà NASA tin chắc có sự sống
-

Xuyên không 55 triệu năm, thế giới giống chúng ta hiện hình
-

Tìm hiểu về bệnh rối loạn phân ly tập thể
-

Miền Bắc sẽ mưa giông từ giữa tuần sau
Câu chuyện khoa học
-

Cuộc sống 50 năm sau: Thọ hơn, khỏe hơn và không cô độc
-

“Bà tiên” đem lại hạnh phúc cho nhiều gia đình
-

Giống lúa cao sản đưa nhà khoa học Việt thắng giải VinFuture 2023
-

3 điều Bill Gates sẽ làm nếu được quay trở lại quá khứ
-

Những tiết lộ gây sốc về nhà độc tài Hitler
-

30 phút đấu trí với Google của chàng trai Việt















