du thuyền không nhiễm ncov
-
 Rồng biển - huyền thoại và sự thực Khi bay sát mặt biển Ấn Độ Dương vào một ngày cuối năm 1968, hai phi công Liên Xô nhìn mấy con quái vật khổng lồ hình rắn. Họ không phải là những người duy nhất gặp "rồng biển", một loài vật mà sự tồn tại đã đư
Rồng biển - huyền thoại và sự thực Khi bay sát mặt biển Ấn Độ Dương vào một ngày cuối năm 1968, hai phi công Liên Xô nhìn mấy con quái vật khổng lồ hình rắn. Họ không phải là những người duy nhất gặp "rồng biển", một loài vật mà sự tồn tại đã đư
-
 Quái vật Kraken có thật? Trong siêu phẩm Cuộc chiến giữa các vị thần ra mắt ngày 9/4 tại Việt Nam có cảnh thần Zeus thét lớn: “Thả Kraken!”. Quái vật Kraken liệu có tồn tại?
Quái vật Kraken có thật? Trong siêu phẩm Cuộc chiến giữa các vị thần ra mắt ngày 9/4 tại Việt Nam có cảnh thần Zeus thét lớn: “Thả Kraken!”. Quái vật Kraken liệu có tồn tại? -
 Cận cảnh chú cá mập trắng khổng lồ với hàng trăm vết sẹo "yang hồ" nhất đại dương Theo đó, chú cá mập với hàng trăm vết thương này đã khiến các nhà nghiên cứu tỏ ra hứng thú ngay từ lần đầu gặp gỡ.
Cận cảnh chú cá mập trắng khổng lồ với hàng trăm vết sẹo "yang hồ" nhất đại dương Theo đó, chú cá mập với hàng trăm vết thương này đã khiến các nhà nghiên cứu tỏ ra hứng thú ngay từ lần đầu gặp gỡ.
-
 4 bí mật chưa có lời giải tại Trung Quốc Trong lịch sử 5000 năm của Trung Quốc, quá nhiều sự tình bí ẩn xuất hiện cho đến nay vẫn không thể lý giải được. Cùng điểm lại 4 sự kiện bí ẩn lớn của quốc gia có nền văn minh từng thuộc hàng đồ sộ bậc nhất thế giới.
4 bí mật chưa có lời giải tại Trung Quốc Trong lịch sử 5000 năm của Trung Quốc, quá nhiều sự tình bí ẩn xuất hiện cho đến nay vẫn không thể lý giải được. Cùng điểm lại 4 sự kiện bí ẩn lớn của quốc gia có nền văn minh từng thuộc hàng đồ sộ bậc nhất thế giới. -
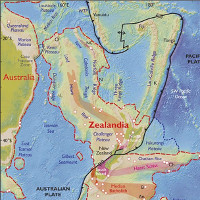 Phát hiện lục địa ngầm gần 5 triệu km2 ẩn dưới Thái Bình Dương Nghiên cứu mới của một nhóm nhà khoa học quốc tế chỉ ra Trái Đất có một lục địa mang tên Zealandia ẩn bên dưới Thái Bình Dương và gắn liền với New Zealand.
Phát hiện lục địa ngầm gần 5 triệu km2 ẩn dưới Thái Bình Dương Nghiên cứu mới của một nhóm nhà khoa học quốc tế chỉ ra Trái Đất có một lục địa mang tên Zealandia ẩn bên dưới Thái Bình Dương và gắn liền với New Zealand. -
 Siêu du thuyền chạy bằng hydro đầu tiên trên thế giới có gì đặc biệt? Với công nghệ mới, khí thải từ du thuyền chạy hydro lỏng sẽ được trung hòa và kết tinh thành nước, thay vì các tạp chất ô nhiễm như chất đốt thông thường.
Siêu du thuyền chạy bằng hydro đầu tiên trên thế giới có gì đặc biệt? Với công nghệ mới, khí thải từ du thuyền chạy hydro lỏng sẽ được trung hòa và kết tinh thành nước, thay vì các tạp chất ô nhiễm như chất đốt thông thường. -
 5 điều ít biết về cá mái chèo Cá mái chèo có xương dài nhất thế giới loài cá, ngoài ra chúng còn có thịt nhão và dính. Đặc biệt loài này hiếm được phát hiện như cách đây không lâu trên bờ biển Mỹ.
5 điều ít biết về cá mái chèo Cá mái chèo có xương dài nhất thế giới loài cá, ngoài ra chúng còn có thịt nhão và dính. Đặc biệt loài này hiếm được phát hiện như cách đây không lâu trên bờ biển Mỹ. -
 Bí ẩn hiện tượng xác chết không phân hủy Hiện tượng thân thể không phân hủy dù cơ thể đã chết hàng trăm năm là một bí ẩn lớn với các nhà khoa học.
Bí ẩn hiện tượng xác chết không phân hủy Hiện tượng thân thể không phân hủy dù cơ thể đã chết hàng trăm năm là một bí ẩn lớn với các nhà khoa học. -
 Kim tự tháp bí ẩn lớn gấp 2 lần Giza được người khổng lồ cao 3m xây dựng? Nằm trên ngọn núi Puela, kim tự tháp bí ẩn mở ra những câu chuyện về kỹ thuật xây dựng các công trình khổng lồ chưa từng được công bố.
Kim tự tháp bí ẩn lớn gấp 2 lần Giza được người khổng lồ cao 3m xây dựng? Nằm trên ngọn núi Puela, kim tự tháp bí ẩn mở ra những câu chuyện về kỹ thuật xây dựng các công trình khổng lồ chưa từng được công bố. -
 Lý giải về các "quái vật" huyền thoại Thế giới còn rất nhiều điều kỳ lạ mà con người chưa khám phá ra. Bên cạnh đó, con người cũng góp phần tạo nên sự kỳ bí của các loài sinh vật lạ lùng qua những lời đồn đại.
Lý giải về các "quái vật" huyền thoại Thế giới còn rất nhiều điều kỳ lạ mà con người chưa khám phá ra. Bên cạnh đó, con người cũng góp phần tạo nên sự kỳ bí của các loài sinh vật lạ lùng qua những lời đồn đại.
 Khoa học quân sự
Khoa học quân sự  Tại sao
Tại sao  Địa danh nổi tiếng
Địa danh nổi tiếng