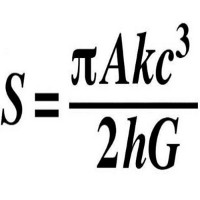17 phương trình này đã thay đổi cả thế giới, bạn nhớ được bao nhiêu cái?

Thời đi học bạn đã được dạy hết về những phương trình này rồi đấy.

Nhà toán học, khoa học nổi tiếng thế giới Ian Stewart đã xuất bản một cuốn sách về "17 phương trình thay đổi thế giới". Đây là những phương trình gắn liền với tất cả học sinh, sinh viên mọi thế hệ, đang được dân mạng lục lại và chia sẻ khắp nơi trên mạng xã hội.

17 phương trình này bao gồm: Định lý Pitago, Logarit, Vi tích phân, Định luật vạn vật hấp dẫn, Căn bậc hai của -1, Đặc trưng Euler, Phân phối chuẩn, Phương trình sóng, Biến đổi Fourier, Hệ phương trình Navier-Stokes, Phương trình Maxwell, Định luật thứ hai của nhiệt động lực học, Sự tương đương của khối lượng và năng lượng, Phương trình Schorodinger, Lý thuyết thông tin, Lý thuyết thông tin, Lý thuyết hỗn loạn, Phương trình Black-Scholes.

Dưới đây là những phương trình quen thuộc nhất, hầu như ai cũng từng được học hoặc gặp ít nhất 1 lần trong cuộc sống.

Định lý Pytago là một liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông ) bằng tổng bình phương của hai cạnh còn lại. Định lý có thể viết thành một phương trình liên hệ độ dài của các cạnh là a, b và c, thường gọi là "công thức Pytago":

Logarit là phép toán nghịch đảo của lũy thừa. Điều đó có nghĩa logarit của một số là số mũ của một giá trị cố định, gọi là cơ số, phải được nâng lên lũy thừa để tạo ra con số đó. Trong trường hợp đơn giản logarit là đếm số lần lặp đi lặp lại của phép nhân. Ví dụ, logarit cơ số 10 của 1000 là 3, vì 10 mũ 3 là 1000 (1000 = 10 × 10 × 10); phép nhân được lặp đi lặp lại ba lần.

Vi tích phân

Công thức trên thể hiện định nghĩa của đạo hàm trong vi tích phân. Đạo hàm thể hiện tốc độ mà một đại lượng đang thay đổi. Ví dụ đơn giản, bạn có thể đã biết vận tốc là đạo hàm của vị trí. Nó thể hiện sự thay đổi vị trí nhanh hay chậm. Nếu bạn đang đi bộ với tốc độ 5 km/h, sau mỗi giờ bạn sẽ thay đổi vị trí của mình trên quãng đường 5 km.

Định luật vạn vật hấp dẫn

Định luật của Newton là một nền tảng đáng ghi nhận trong lịch sử khoa học. Nó giúp con người giải thích một cách hoàn hảo sự di chuyển của các hành tinh. Tính chất phổ quát của phương trình này trải dài từ các hiện tượng trên Trái Đất, trong Hệ Mặt Trời tới bất kì đâu trong vũ trụ.

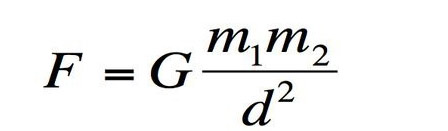
Căn bậc hai của -1

Căn bậc hai của -1, thường được kí hiệu là i, hoàn tất tập hợp số bằng cách tạo ra các số phức.

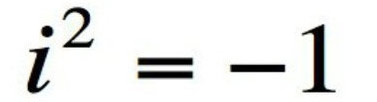
Định luật thứ hai của nhiệt động lực học

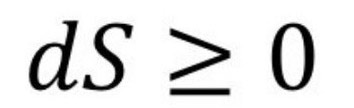
Nguyên lý này khẳng định rằng trong một hệ khép kín, entropy (hiểu một cách đơn giản là sự hỗn loạn) chỉ có thể giữ nguyên hoặc tăng lên. Nghe có vẻ đơn giản nhưng nó chính là một hòn đá tảng chặn đường chúng ta đến với tương lai của những thiết bị viễn tưởng.

Định luật 2 nhiệt động học có thể được sử dụng để dự đoán số phận vũ trụ. Nó giải thích cho sự hỗn loạn của vũ trụ từ sau vụ nổ Big Bang và dẫn đến "cái chết nhiệt" của nó, khi vạn vật cân bằng trên một trạng thái nhiệt độ.

Sự tương đương của khối lượng và năng lượng

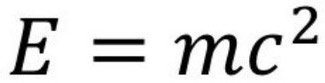
Phương trình này được Einstein đưa ra vào năm 1905 trong một bài báo khoa học với tiêu đề "Quán tính của một vật có phụ thuộc vào năng lượng trong nó không?".

Einstein chứng minh năng lượng và khối lượng vốn chỉ là một. Chúng ở hai trạng thái khác nhau và khối lượng chính là dạng "đặc lại" của năng lượng. Chỉ cần nửa cân bất kỳ chất gì cũng đang chứa trong nó năng lượng tương đương vụ nổ của hơn 7 triệu tấn thuốc nổ TNT.

Phương trình E=mc2 giải thích tại sao Uranium lại có thể liên tiếp, trong hàng triệu năm, bắn ra những tia li ti chạy với tốc độ khủng khiếp, tại sao mặt trời và các ngôi sao có thể tuôn ánh sáng và sức nóng trong hàng tỷ tỷ năm.

Nó còn cho chúng ta thấy năng lượng ghê gớm chứa trong nhân nguyên tử và tiên đoán chỉ cần một lượng rất nhỏ Uranium cũng đủ tạo ra một trái bom có sức công phá hủy diệt cả một thành phố.